
Simply because we observe a relationship between two variables in a scatter plot, it does not mean that changes in one variable are responsible for changes in the other. This is not so much an issue with creating a scatter plot as it is an issue with its interpretation. Heatmaps in this use case are also known as 2-d histograms. As a third option, we might even choose a different chart type like the heatmap, where color indicates the number of points in each bin. We can also change the form of the dots, adding transparency to allow for overlaps to be visible, or reducing point size so that fewer overlaps occur.
#XY SCATTER CHART FULL#
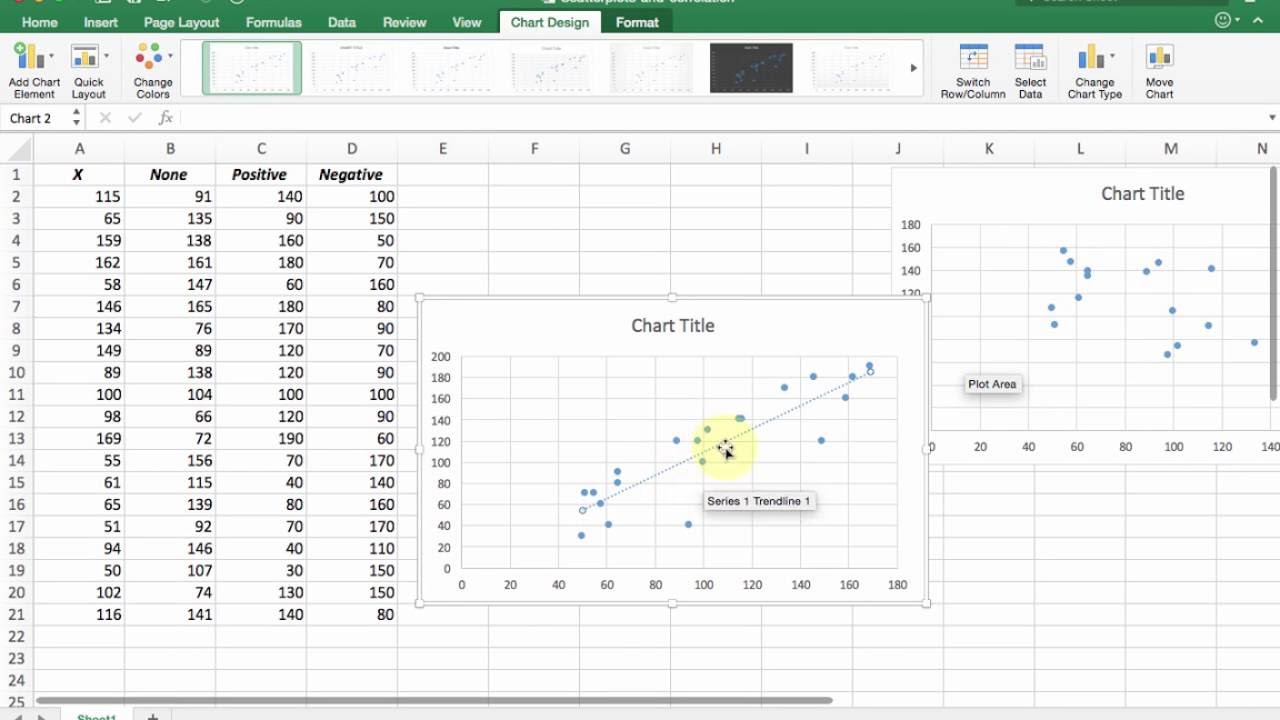
One alternative is to sample only a subset of data points: a random selection of points should still give the general idea of the patterns in the full data. There are a few common ways to alleviate this issue. It can be difficult to tell how densely-packed data points are when many of them are in a small area. Overplotting is the case where data points overlap to a degree where we have difficulty seeing relationships between points and variables. When we have lots of data points to plot, this can run into the issue of overplotting. Common issues when using scatter plots Overplotting Each row of the table will become a single dot in the plot with position according to the column values. In order to create a scatter plot, we need to select two columns from a data table, one for each dimension of the plot. This can be useful if we want to segment the data into different parts, like in the development of user personas. Scatter plots can also show if there are any unexpected gaps in the data and if there are any outlier points. We can divide data points into groups based on how closely sets of points cluster together. Relationships between variables can be described in many ways: positive or negative, strong or weak, linear or nonlinear.Ī scatter plot can also be useful for identifying other patterns in data. You will often see the variable on the horizontal axis denoted an independent variable, and the variable on the vertical axis the dependent variable. In these cases, we want to know, if we were given a particular horizontal value, what a good prediction would be for the vertical value. Identification of correlational relationships are common with scatter plots. The dots in a scatter plot not only report the values of individual data points, but also patterns when the data are taken as a whole. Scatter plots’ primary uses are to observe and show relationships between two numeric variables. This tree appears fairly short for its girth, which might warrant further investigation. We can also observe an outlier point, a tree that has a much larger diameter than the others. From the plot, we can see a generally tight positive correlation between a tree’s diameter and its height. Each dot represents a single tree each point’s horizontal position indicates that tree’s diameter (in centimeters) and the vertical position indicates that tree’s height (in meters). The example scatter plot above shows the diameters and heights for a sample of fictional trees. Scatter plots are used to observe relationships between variables. The position of each dot on the horizontal and vertical axis indicates values for an individual data point. With an RMS error of 0.02 for the coefficients shown below.A scatter plot (aka scatter chart, scatter graph) uses dots to represent values for two different numeric variables. That's a rational function, not a polynomial.
#XY SCATTER CHART CODE#
(autolink killer: 2007 AI attached array case cell chain changes code CodeName combos Count CountBlank COUNTIF Date database Delete error F8 filter Find formula Function import link merge methods Move MsgBox multiple Name named nest Object Password pivot range record reference rounding SaveAs ScreenUpdating Search Sheet sort Step times ThisWorkbook total tracking unprotect Validation VLookup Worksheet) Re: Finding The Equation Of A Smooth Xy Scatter


 0 kommentar(er)
0 kommentar(er)
